Polynomials
Information
In order to find the roots of a polynomial we first need to look at the quadratic formula (shown below) which allows us to quickly find the roots to a quadratic equation (a polynomial up to x2)
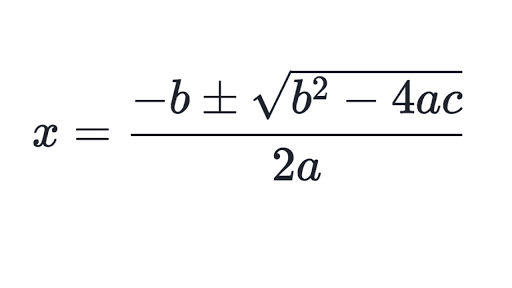
In order to use the quadratic formula we first must know that:
a represents the coefficient of x2
b represents the coefficient of x
c represents the constant
e.g. in the polynomial 3x2 + 2x + 1
a = 3, b = 2, c = 1
Introducing Complex Numbers
A complex number is a number that has both a real and imaginary part
The real part are the numbers we normally see such as integers, fractions and roots
The imaginary part is where there is a √-1 also known as i (i = √-1)
An example of where you might see a complex number is the root of a polynomial such as
x2 - 4x + 5
Inputting a = 1, b = -4 and c = 5 into the quadratic formula gives us the roots:
x = 2 + i and 2 - i
This is called a complex conjugate (a pair of complex numbers), this will always be the case where if you have a root of 2 + i you will have the complex conjugate of 2 - i
This can also be written down as 2 ± i
(i = √-1, i2 = -1, i3 = -√-1 = -i)
*Important*
The complex conjugate of z is z*
where z represents a complex number
Finding Roots in Cubic Equations
When confronted by a cubic equation we are unable to use the quadratic equation as there are now 3 roots to the equation and not 2 roots
We instead have to employ a different strategy to find the roots shown easily in an example
If we have the cubic equation of:
x3 - x2 - 8x + 12
We first find the factors of the constant 12 which are:
±1, ±2, ±3, ±4, ±6, ±12
We then input these factors in the place of x until the equation = 0 such as:
(1)3 - (1)2 - 8(1) + 12 = 0
1 - 1 - 8 + 12 = 0
4 = 0 as this is not true (x-1) is not a factor so we move onto the next factor
(2)3 - (2)2 - 8(2) + 12 = 0
8 - 4 - 16 + 12 = 0 which is true so (x - 2) is a root
(If no positive factor leads to the equation being true switch to the negative factors)
We then need to divide the original equation by (x - 2)
This leaves us with the equation (x-2)(x2 + x - 6)
Using the quadratic formula to find the roots of x2 + x - 6 we find that:
(x - 2)(x - 2)(x + 3) = 0
Meaning the roots of the equation are:
x = 2, x = 2 and x = -3
As only when x is these values the equation is true